统计过程控制（SPC）直方图分析

摘要：直方图是针对某产品或过程的特性值，利用常态分布（也叫正态分布）的原理，把50个以上的数据进行分组，并算出每组出现的次数，再用类似的直方图形描绘在横轴上。

直方图
    直方图 是针对某产品或过程的特性值，利用常态分布（也叫正态分布）的原理，把50个以上的数据进行分组，并算出每组出现的次数，再用类似的直方图形描绘在横轴上。
通过直方图，可将杂乱无章数据，解析出规则性，也可以一目了然地看出数据的中心值及数据的分布情形。
    在制造业，现场的管理干部经常都要面对许多数据，这些数据大多来自制造加工过程的抽样测量得到，对于这些凌乱的数据，如果制作成直方图，并借助对直方图的观察，可以了解产品质量分布的规律，知道其是否变异，并进一步分析判断整个生产过程是否正常，问题点在哪里，为研究 过程能力 提供依据。

通过直方图，可以达到的目的
• 了解质量分布的状况，对质量状况分析有极其重要的参考价值；
• 显示波动的形态，知道其是否变异；
• 直观地传达有关过程质量分布情况的信息；
• 观察产品质量在某一时间段内的整体分布状况；
• 研究过程能力或预测过程能力；
• 求分配的平均值和标准值；
• 调查是否混入两个以上的不同群体；
• 测知是否有虚假数据
• 制定产品的规格界限；

直方图（频数分布图）的制作步骤
• 收集同一类型的数据；
• 计算极差（全距）；
• 设定组数，计算组距、组界、中心值；
• 制作频数表；
• 按频数值比例画横坐标、纵坐标；
• 按纵坐标画出每个矩形的角度，代表落在此矩形中的点数；
• 判续 直方图 （对过程状态分析）。

直方图的常见形态与判定
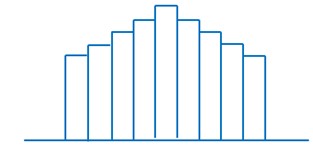
1）正常型：是正态分布，服从统计规律，过程正常。

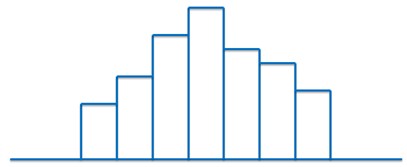
2）缺齿型：不是正态分布，不服从统计规律，可能的原因是:
• 有经验的人员故意做的假数据。
• 测量仪器精确度不够，而要求的精确度较高，检验员只好进行估计。
• 较多特性差异的数据混杂在一起。

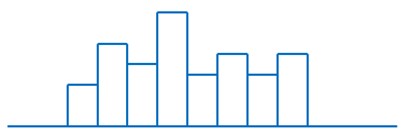
3）偏态型：不是正态分布，不服从统计规律，可能的原因是：
• 习惯作业造成作业方法不对。
• 工具、夹具、模具已经磨损或松动。

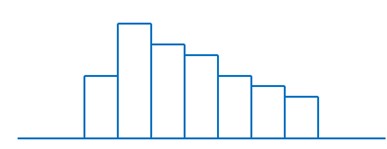
4）离岛型：不是正态分布，不服从统计规律，可能的原因是:
• 数据输入人员在输入的过程中，可能把10.01输 10.10或1.01。
• 过程中其他物料混入。
• 机台设备在过程中出现特殊原因，产生了变异。

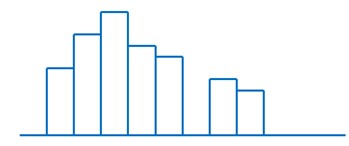
5）高原型：不是正态分布，不服从统计规律，可能的原因是：
• 人员做的假数据。
• 经过全检挑选的数据。
• 测量仪器精确度不够。